こんばんは。 10連休もあと1日となりました。いかがお過ごしでしょうか。
私は連休半ばで何も成せていないことに気づき、生活習慣を改めることにしました。
Twitterからログアウトした上で、Twitterアカウントのパスワードを保存してあるパスワード管理ツールの2段階認証のトークンをつくばに置いて長野に帰省します。強制的なTwitter断ちをする。
— 杉山 将利 (@smasat0) May 2, 2019
そんな中、Twitterを制限するのも兼ねて実家に帰省し、本を読むなどして過ごしていると現状の大学生活に危機感をこれまでよりも強く感じました。 それは、卒業に必要な数学の必修科目の単位を何一つ修得できていないということです。
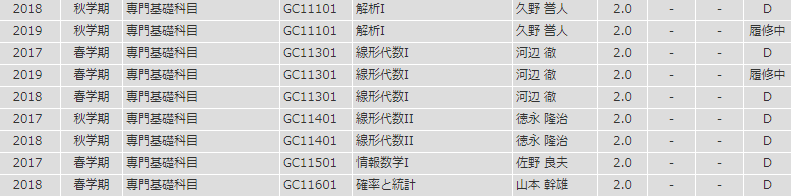
「いや、2年間なにしてたのさ」という話なのですが、ひとまず置いておいてください。
なぜこのような状況になっているのか3行で説明すると、
- 中学2年生の夏休み明けから不登校になり復帰することなく卒業
- 全日制の高校に入学するも諸般の事情により通信制高校に転入学
- 高校では数学を最小限しか勉強しなかった
- センター試験を必要としない入試で大学に合格
という経緯があります。3行では説明できませんでした……
そして、およそ5年間の数学のブランクをそのままに大学の授業に臨み完全に打ちのめされました。 1年目はされるがままままに単位を落としたわけですが、それを受けても長すぎるブランクに向き合うことができず、ほとんど対策をしない状態で2年目も授業を受け単位を落としました。
同じ敵に2度も負けました。弱くてニューゲームなので当然です。
ところで、大学はほとんどの場合は4年間で卒業するものです。 これまでの2年間であまりにも単位が取れていないので、一度、2年間を無かったことにしてみると大変なことが明らかになります。
なんとあと4年間しか大学にいられないのです。
筑波大学は6年間の在籍期間がありますが、もう既に2年間を使っているため、残りは4年間になっています。つまりは今年から心を入れ替えて1年生で修得すべき単位を順に履修していかなければ、大雑把に考えると多分卒業できないということです。履修を詰め込めば余裕があるのかもしれませんが、これまでのことを考えると現実的ではありません。
負けられない戦い、開戦
前置きが長くなりましたが、今年は数学の単位を何としても取らなければならなくなりました。ついに切羽詰まりました。
本題です。
数学の授業を受けたり勉強したりすると憂鬱になり気持ちが落ち込むほどに数学への苦手意識や嫌悪感があるため、どうしたら勉強すればいいのかわかりませんでした。
ただ、今期履修している線形代数の授業をまずはなんとかしなければいけないことはわかっています。
実家にいた昨日、父親と一緒にこれまでの授業の演習問題を解説を読みながら解きなおしてみましたがベクトルの内積がどうしても理解できませんでした。 ベクトルの内積についての解説を検索してみましたが納得ができませんでした。
その時、予備校のノリで学ぶ「大学の数学・物理」というチャンネルを思い出しました。 このチャンネルは大学の先輩に次の動画を教えていただいたことで知りました。
まさに私のためではないかと思うほどドンピシャの動画で、とてもわかりやすかったことが印象に残っています。
このチャンネルにベクトルについての動画がないかと探してみると次の動画が見つかりました。
このシリーズではベクトルの内積の解説はありませんでしたが、ほかの線形代数の動画を見ていくとこれまでの授業で聞いたことを理解することができ、線形代数が面白いと思えてきました。
ベクトルの内積についてはわからないままだったのでいい解説がないか探していると、「数学ガールの秘密ノート」シリーズにベクトルをテーマにした巻がありました。読んだことのある父親に聞いてみると、この本の内積の説明なら理解できるだろうとのことだったので買って読んでみることにしました。

数学ガールの秘密ノート/ベクトルの真実 (数学ガールの秘密ノートシリーズ)
- 作者: 結城浩
- 出版社/メーカー: SBクリエイティブ
- 発売日: 2015/11/18
- メディア: 単行本
- この商品を含むブログ (11件) を見る
また、秘密ノートシリーズの他の巻も大学の数学に関係がありそうだったので既に買っていた「行列が描くもの」以外の8巻も「ベクトルの真実」と合わせてkindle版をまとめ買いしました。
そして今日、「ベクトルの真実」を読み始めました。 つくばへのバスの中でも読んでいたとき、数学がイヤでなくなる出来事が起こりました。
まさにベクトルの内積についての説明が納得できず、気づくとノートに自分の中で疑問を整理するために20分ほど数式を書いたり消したりしていました。それでもわかりませんでしたが。
自分では最終的に納得できませんでしたが、この20分間は間違いなく数学が楽しかったのです。疑問を感じてからノートで試行錯誤をしていた20分間はあっという間でした。
どうしても気になったので著者の結城先生にTwitterで質問してみることにしました。
@hyuki こんにちは。「数学ガールの秘密ノート ベクトルの真実」の176ページの説明について考えていたのですが、画像のような流れでよくわからなくなってしまいました。お時間があればどこが間違っているのか教えていただけると嬉しいです。 pic.twitter.com/pjHjFCzWFD
— 杉山 将利 (@smasat0) May 5, 2019
すると、なんと丁寧に解説をしてくださり、この点については納得できました。
計算自体は間違っていません。cosθ=cosθはただしいですから。
— 結城浩 (@hyuki) May 5, 2019
ここは「何を定義して何を得るか」の発想の話です。
通常は、ベクトルの大きさと角度を定義して(既知として)、内積という量を求めるわけです。(続く)
著者の結城先生から自分の質問への解説をいただけたことがとても嬉しかったです。
ヨビノリの動画で線形代数が面白いと思えたこと、数学ガールの秘密ノートで理解が深まったことが重なり起きた小さな出来事ですが、あの20分で数学への苦手意識や嫌悪感は氷解した気がしています。やればできる、面白いという気持ちで数学に向き合うことができそうです。今のところは。
この気持ちを大事にしたほうがいいと思いこの記事を書きました。
単位が取れるように頑張ります。